The Null Hypothesis - H0:  γ₁ = γ_{2 = ...  =}  0  i.e.  there is no heteroscedasticity in the model

The Alternative Hypothesis - H1:  at least one of the γ_i's are not equal to zero i.e. the squared residuals are related to one of the independent variables.

Reject H0 if nR² >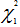

MTB > let c23 = c7*c7

MTB > let c24 = c8*c8

MTB > let c25 = c9*c9

MTB > let c26 = c10*c10

MTB > let c27 = c7*c8

MTB > let c28 = c7*c9

MTB > let c29 = c7*c10

MTB > let c30 = c8*c9

MTB > let c31 = c8*c10

MTB > let c32 = c9*c10

C7 = totexp

C8 = income

C9 = age

C10 = nk

C23 = sqtotexp

C24 = sqincome

C25 = sqage

C26 = sqnk

C27 = totexpincome

C28 = totexpage

C29 = totexpnk

C30 = incomeage

C31 = incomenk

C32 = agenk

Regression Analysis: sqres versus totexp, income, ...

* sqnk is highly correlated with other X variables

* sqnk has been removed from the equation.

The regression equation is

sqres = 0.0178 - 0.000232 totexp + 0.000023 income + 0.000298 age - 0.00555 nk

        + 0.000001 sqtotexp + 0.000000 sqincome - 0.000005 sqage

        - 0.000000 totexpincome + 0.000003 totexpage + 0.000015 totexpnk

        - 0.000001 incomeage + 0.000035 incomenk - 0.000021 agenk

Predictor            Coef     SE Coef      T      P

Constant         0.017804    0.007900   2.25  0.024

totexp        -0.00023207  0.00005370  -4.32  0.000

income         0.00002344  0.00003865   0.61  0.544

age             0.0002978   0.0003511   0.85  0.396

nk              -0.005551    0.003233  -1.72  0.086

sqtotexp       0.00000060  0.00000011   5.65  0.000

sqincome       0.00000004  0.00000002   1.79  0.074

sqage         -0.00000464  0.00000427  -1.09  0.277

totexpincome  -0.00000041  0.00000013  -3.27  0.001

totexpage      0.00000259  0.00000110   2.36  0.018

totexpnk       0.00001477  0.00001740   0.85  0.396

incomeage     -0.00000110  0.00000090  -1.22  0.223

incomenk       0.00003506  0.00001355   2.59  0.010

agenk         -0.00002146  0.00008647  -0.25  0.804

S = 0.0123952   R-Sq = 3.4%   R-Sq(adj) = 2.5%

Analysis of Variance

Source            DF         SS         MS     F      P

Regression        13  0.0080446  0.0006188  4.03  0.000

Residual Error  1505  0.2312304  0.0001536

Total           1518  0.2392750

Source        DF     Seq SS

totexp         1  0.0003007

income         1  0.0000070

age            1  0.0000053

nk             1  0.0000429

sqtotexp       1  0.0037616

sqincome       1  0.0000507

sqage          1  0.0001055

totexpincome   1  0.0010903

totexpage      1  0.0005678

totexpnk       1  0.0009260

incomeage      1  0.0001557

incomenk       1  0.0010217

agenk          1  0.0000095

MTB > let k4=1519*0.034

MTB > print k4

Data Display

K4    51.6460

MTB > InvCDF 0.95;

SUBC>   ChiSquare 13.

Inverse Cumulative Distribution Function

Chi-Square with 13 DF

P( X <= x )        x

       0.95  22.3620

MTB > # Since nrsq = 1519*0.034= 51.6460 > chi=22.360 we have hetero from white test# Also both B-P and White test seem to indicate that totexp is the culprit

Since nrsq = 51.6460 > 22.360 = , there is sufficient evidence to reject H0 which suggests that there is heteroscedasticity in the model from White's general heteroscedasticity test at the 5% significance level.  Both Breusch Pagan test and White's general heteroscedasticity test seem to indicate that totexp is the culprit as the T value is significant and the P-value is 0.000.