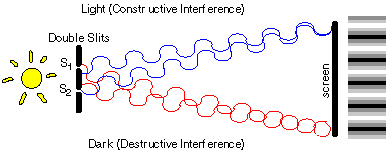
What is the Interference?
A single frequency light passing through a pair of closely spaced slits will show a pattern of vertical bands, due to alternating constructive and destructive interference between the coherent light from the two slits. Constructive interference and the resulting bright band happens when the difference between the path from one slit and from the other is λ, 2λ, 3λ, 4λ, etc. A dark band, due to destructive interference, happens when the path difference is λ, 3/2λ, 5/2λ, 7/2λand so on.
The wavelength of the light can be calculated from the distance between the center and the first bright band on the screen.
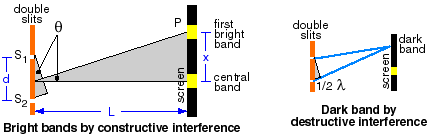
The length of light path S1P and the light path S2P must have a difference of one λ in order to have constructive interference. If L, the distance to the screen, is much larger than d, the distance between the slits, so that θ is very small and θ is about equal to sin θ:
Sin θ = X/L = λ/d so that λ = d (X/L)
where θ is the angle between the central and first bright band, λ is the wavelength of the light, x is the distance along the screen to the first bright band, d is the distance between the two slits, and L is the distance from the slits to the screen.
Moire patterns, which are the changing patterns you see when you overlap two transparencies with thin stripes, are a consequence of interference. You can see them when you look through two chain link fences as you pass them in a car.
In various thicknesses of thin films, different colors of light are able to constructively interfere when the path difference between light reflected from the top surface and from the bottom surface matches the light's wavelength, causing the changing stripes of color we see in soap bubbles, the thin films of oil on puddles, and the colored bands on a CD. A layer of thickness, t, of ink is placed on the CD surface and then ruled with concentric circles of information. As you view the reflection at larger angles, the path difference becomes larger and a longer wavelength of light will be able to constructively interfere as well, and more bands of color will appear.
Newton's rings are a very precise way to measure the curvature or flatness of a piece of glass. The light reflecting from the bottom of the lens interferes with the light from the top of the flat glass plate, creating concentric rings.