Q. What is Frequency Translation and Product Modulation?

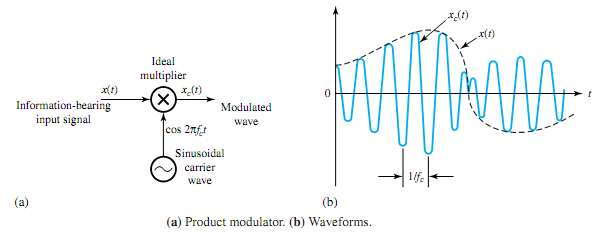
The basic operation needed to build modulators is the multiplication of two signals. Whenever sinusoids are multiplied, frequency translation takes place. Figure 14.2.1(a) shows a product modulator, which multiplies the signal x(t) and a sinusoidal carrier wave at frequency fc to yield

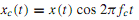
Choosing x(t) to be a low-pass signal with bandwidth W << f_c, Figure (b) depicts the relationship between x_c(t) and x(t). The modulated wave x_c(t) can now be seen to have a bandpass spectrum resulting from frequency translation, which will be explained later. If x(t) contains a sinusoidal component Am cos 2πfmt, multiplication by a sinusoidal carrier wave cos 2πfct with fc >> fm yields

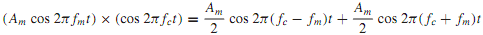
Waveforms of the signal, the carrier wave, and the product, as well as their respective line spectra, are shown in Figure. Notice that the low frequency fm has been translated to the higher frequencies fc ± fm.

Next, let us consider an arbitrary low-pass signal x(t) with the typical amplitude spectrum of Figure. The amplitude spectrum of the modulated wave x_c(t) will now have two sidebands (lower and upper sidebands), each of width W on either side of f_c, as illustrated in Figure. Thus, we have a signal that can be transmitted over a bandpass system with a minimum bandwidth of which is twice the bandwidth of the modulating signal. This process is then known as double-side band modulation (DSB). Either the lower or the upper sidebandmay be removed by filtering so as to obtain single-sidebandmodulation (SSB) with B=W, if the bandwidth needs to be conserved.

By choosing the carrier frequency f_c at a value where the system has favorable characteristics, the frequency translation by product modulation helps in minimizing the distortion and other problems in system design.