Q. What happens to the energy values of d- orbitals?

Let us see what happens to the energy values of d- orbitals under these stages. We start with the energy level diagram of a lower triplet (t2J and upper doublet (_eg) in an octahedral field. Fig. When the two Trans ligands placed along pay, z-axis, are moved away the most affected orbital would be d_z2. The repulsion between the orbital and the ligand will decrease, thus making it more stable compared to others. At the same time all other orbitals containing z-axis namely d_xy, d_yz will also be affected by the movement of the two ligands - along the z-axis. However, these will experience less effect than the d_z2 orbital. These two orbitals will become lower in energy by equal amount but less than d_z2 as indicated by different slopes in Fig.

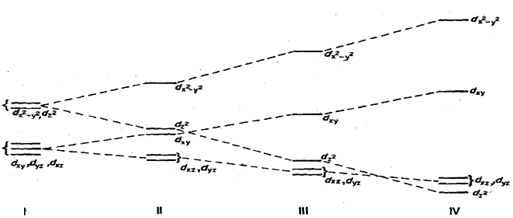
For _eg set of orbitals, if d² orbital lowered energy due to distortion, then d_x2 -_y2 must go  ~p in energy by an equal amount 40 that the net result is no change. Similarly, d_xz and d_yz are  lowered whereas d_xy is raised in energy by such an amount that the net resultant is zero. Thus  in a distorted octahedral molecule the orbitals in order of Increasing energy or  decreasing stability are : d_xz, d_yz)- (degenerate), GI d_xy, d_z2 - _y2 as shown in Fig. (113. A further distortion results in the formation of a square planar complex. Here, d_z2 is lowered so much SO that it is almost equal to d_xy, d_yz orbitals Fig. (111). Much higher will be d_xy  and the least stable or the highest in energy would be d,2 - )2. In a few rare instances dz2 falls even below d,, and d,, orbitals Fig. (IV). We realise that in case of a square planar complex we shall not be able to calculate quantitatively the energy values of the orbitals in terms of crystal field splitting parameter (4). The actual values have. However, been calculated; based on these values we can calculate CFSE as well as the magnetic moment for any particular complex. It has been observed that at least the first row transition elements show greater tendency to form square planar rather than tetrahedral complexes. These observations are in line with the CFSE calculations for the two geometries.

We have thus come to the stage where we can appreciate that a simple electrostatic approach can lead to many useful results and these results are pretty close to the experimental values.  We do not expect to get perfect results since our assumptions so far are imperfect. We are, thus, left with two choices either to discard the theory completely and look for a new approach or to modify it in such way so as to account for the observed discrepancies.