Q. What do you mean by Waveforms?

We are often interested in waveforms, which may not be constant in time of particular interest is a periodic waveform, which is a time-varying waveform repeating itself over intervals of time T> 0.

f(t) = f(t ± nT ) n = 1, 2, 3, ···

The repetition time T of the waveform is called the period of the waveform. For a waveform to be periodic, it must continue indefinitely in time. The dc waveform of Figure(a) can be considered to be periodic with an infinite period. The frequency of a periodic waveform is the reciprocal of its period,

f =  1/T Hertz (Hz)

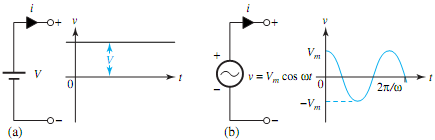
A sinusoidal or cosinusoidal waveform is typically described by

f(t) = A sin(ωt + φ)

where A is the amplitude, φ is the phase offset, and ω = 2πf = 2π/T is the radian frequency of the wave. When φ = 0, a sinusoidal wave results, and when φ = 90°, a cosinusoidal wave results. The average value of a periodic waveform is the net positive area under the curve for one period, divided by the period,