Q. What do you mean by Amplifier block?
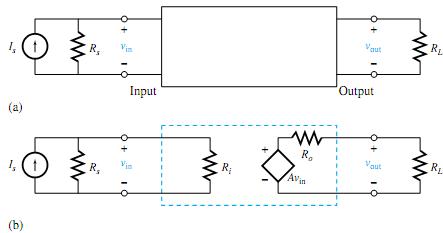
An amplifier can be modeled as a two-port device, that is, a box with two pairs of terminals designated as input and output, as shown in Figure (a). The circuit model of the amplifier block shown in Figure (b) is developed on the basis of the following considerations:
1. Since, for most amplifiers, the input current is proportional to the input voltage, the input terminals in the model are connected by a resistance Ri, known as the input resistance of the amplifier.
2. Since an amplifier delivers electric power (to a speaker, for example), the output current can be represented by its Thévenin-source model. The Thévenin resistance Ro is known as the output resistance and the Thévenin voltage is a dependent voltage source Avin, where A is called the open-circuit voltage amplification.
Thus, the amplifier block is a linear circuit block in which the output is proportional to the input, and the amplifier is characterized by the three constants Ri,Ro, and A. The input and output resistancesmay be generalized to input and output impedances in ac systems. The advantage of the model is that all internal complexities are summarized in the three constants, thereby simplifying the analysis of electric systems with amplifiers. Power-supply connections are usually not shown in circuit diagrams since they would only clutter up the drawing. It is assumed, however, that there are always connections to some power source in order to bring in the power necessary to run the amplifier.