What are Factor Trees explain?
In algebra, we often need to factor a number into its prime factors. One way to do this is to use a factor tree. This is a network of numbers, starting with one number at the top of the tree, with factors branching downward from it. At each stage, each factor is broken down into smaller factors until only the prime factors are left.
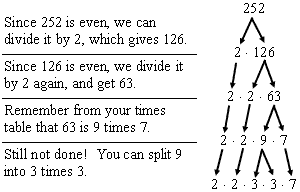
Example: Write the prime factorization of 252.
See if you can write the prime factorization of 150.
When using a factor tree, it doesn't matter which two factors you use to begin. For example, when you did your factor tree for 150, you may have chosen to start with the factors 2 and 75 or the factors 3 and 50. Trees for the prime factorization of 150 may look different, but the prime factors come out the same.
Traditionally, the factors in a prime factorization are written in numerical order (smallest to largest).
Also, exponential form may be used to emphasize how many times a prime factor appears in a prime factorization.
So, the prime factorization of 150 is 2 x 3 x 5 x 5 or 2 x 3 x 52.
There is a more systematic way to find the prime factors of a composite number. The idea is to consistently divide the original number and then the result of each division by the smallest possible prime number until only a prime number remains.
One advantage to this method is that the prime factors automatically appear in numerical order.
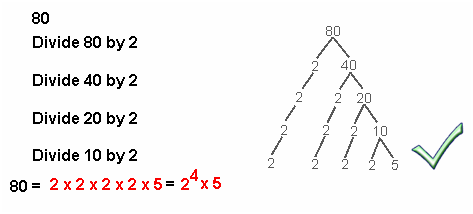
Here is one example.
To find the prime factorization of the number 80: