In order to compute the inequalities of the form

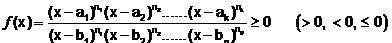
where n₁, n₂, ....... , n k , m₁, m₂, ....... , m_p are natural and real numbers and a₁, a₂, ... , a_k, b₁, b₂, ..., b_p are any real number such that ai ≠ bj where i = 1, 2, 3, ....k and j = 1, 2, 3, ....p.

Method:

Step - 1 First place all values of x at which either denominator or numerator is becomes zero, that denotes a1, a2,....., ak, b1, b2, ....bp in ascending order say c₁, c₂, c3,....... c_p + k. draw them on real line

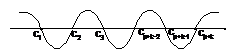
Step -2  Value of x number at which numerator tends to zero could be remarked with dark circles.

Step - 3  All pints of discontinuities (x at which denominator tends to zero) could be remarked on number line with empty circles. Calculate the value of f(x) for any real number bigger than the right most checked number on the number line.

Step - 4  From right to left presented a wavy curve (beginnings above the number line in type of value of f(x) is positive in step-3 otherwise from below the number line), going thoroughly all the checked points. So that when goes through a point (exponent whose related factor is odd) intersects the number line, and when going thoroughly a point (exponent whose related factor is even) the curve doesn't cut the real line and stay on the similar side of real line.

Step - 5 The suitable intervals are selected in accordance with the sign of inequality (the function f(x) is positive wherever the curve is over the number line, it is negative if the curve is searched below the number line). Their union shows the solution of inequality