Vector Function

The good way to get an idea of what a vector function is and what its graph act like is to look at an instance.  Thus, consider the following vector function.

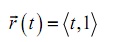
A vector function is a function which takes one or more variables, one in this case, and returns a vector.  Note also that a vector function can be a function of two or more than two variables.  Though, in those cases the graph might no longer be a curve in space.

The vector that the function provides can be a vector in whatever dimension we require it to be.  In the instance above it returns a vector in R².  While we get to the real subject of this section, equations of lines, we will be using a vector function which returns a vector in R³.

Here now, we want to find out the graph of the vector function above.  To find the graph of our function we'll think of the vector that the vector function returns like a position vector for points on the graph.  Remind that a position vector, say, ¯v = (a,b) is a vector that begins at the origin and ends at the point  (a,b).  

 Thus, to get the graph of a vector function all we require to do is plug in some values of the variable and after that plot the point that corresponds to each position vector we get out of the function and play connect the dots.  Now here are some evaluations for our instance.

Thus, each of these are position vectors presenting points on the graph of our vector function.  The points,

are all points that lie on the graph of our vector function. 

If we do some other evaluations and plot all the points we obtain the subsequent sketch.

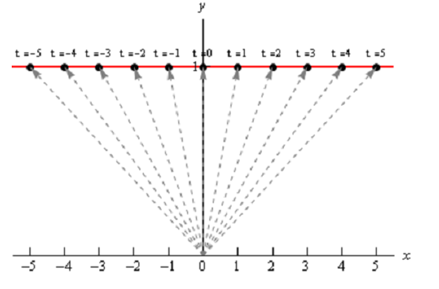
In this diagram we've included the position vector (in gray and dashed) for various evaluations also the t (above each point) we employed for each evaluation.  It looks like, in this case the graph of the vector equation is in fact the line  y =1.