Chain Rule : Assume that we have two functions f(x) & g(x) and they both are differentiable.

1.   If we define F ( x ) = ( f o g ) ( x ) then the derivative of F(x) is,

                            F ′ ( x ) = f ′ ( g( x )) g′ ( x )

2.   If we have y = f (u ) and u = g ( x ) then the derivative of y is,

                     dy /dx= dy / du  .du/  dx

Each forms have their uses, though we will mostly work with the first form in this class.

Now, use the Chain Rule on the function which we used while we opened this section.

Example:  Utilize the Chain Rule to differentiate

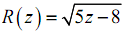
Solution : Already we've identified the two functions that we required for the composition, however let's write them back down anyway & take their derivatives.

f ( z ) =√z                           g ( z ) = 5z - 8

f ′ ( z ) =1/2 √ z                  g′ ( z ) =5

Thus, by using the chain rule we get,

R′ (z ) = f ′ ( g ( z )) g′( z )

=f ′ (5z - 8) g′ ( z )

= 1/2 (5z - 8)^-(1/2)(5)

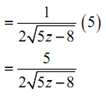
And it is what we got by using the definition of the derivative.