Two people on bikes are at a distance of  350 meters.  Person A begin riding north at a rate of 5 m/sec and 7 minutes later on Person B begin riding south at 3 m/sec.  Determine the rate of the distance separating the two people changing 25 minutes after Person A begin riding?

Solution

There is a many digest here along this problem.  Let's begin with a sketch of the situation.

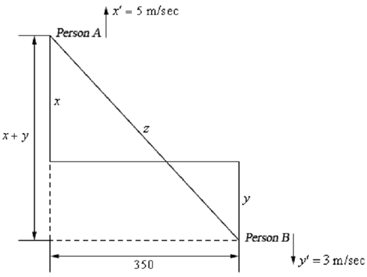
Now we are after z′ & we know that x′ =5 & y′ = 3 .  We desire to know z′ after Person A had been riding for 25 minutes & Person B has been riding for 25 - 7 = 18 minutes.  After turning these times to seconds (Since our rates are all in m/sec) it means that at the time we're interested in each bike riders has rode,

 x = 5 ( 25 × 60) = 7500 m                   y = 3(18 ×60) = 3240 m

Next, using Pythagorean theorem

z ²  = ( x + y )² + 350²

Hence, 25 minutes after Person A begin riding the two bike riders are

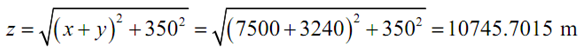
apart.

To find out the rate at which the two riders are moving separately all we have to do then is differentiate (2) and plug in all the quantities which we know to determine z′ .

2zz′ = 2 ( x + y ) ( x′ + y′)

2 (10745.7015) z′ = 2 (7500 + 3240) (5 + 3)

z′ = 7.9958 m/sec

Thus, the two riders are moving separately at rate of 7.9958 m/sec.