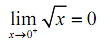Use the definition of the limit to prove the given limit.

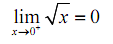
Solution

Let ε> 0 is any number then we have to find a number δ > 0 so that the following will be true.

| √x - 0| < ε               whenever           0 < x - 0 < δ

Or upon a little simplification we need to show,

√x < ε               whenever       0 < x < δ

Let's begin with the left hand inequality and illustrates if we can't utilizes that to get a guess for δ .  The only simplification which we really have to do here is to square both sides.

√x < ε               whenever       x < δ²

Hence, it looks like we can chose δ = ε ² .

Let's verify this.  Let ε > 0 be any number and select δ = ε ² ..  Next suppose that 0 < x < ε ². it gives,

|√x -0|= √x           some quick simplification

      < (√ ε)²        use the assumption that    |x|   < ε

        = ε            simplify

Now we illustrated that,

|√x - 0| =         √x           whenever     0 < x - 0 < ε ²

and therefore by the definition of the right-hand limit we have,