Unit circle: The unit circle is one of the most valuable tools to come out in trig.  Unluckily, most people don't study it as well.

Below is the unit circle with just the first quadrant filled in is represented. The process the unit circle works is to draw a line from the center of the circle outside corresponding to a given angle. Then notify at the coordinates of the point where the line & the circle intersect. The first coordinate is the cosine of that angle & the second coordinate is the sine of that angle. We've put some of the basic angles along with the coordinates of their intersections on the unit circle.  Hence, from the unit circle below we can illustrates that cos (? /6 ) = √3 /2 and sin (?/6)= 1/2 .

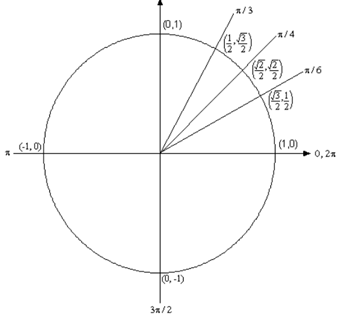
Keep in mind how the signs of angles work.  If you rotate into a counter clockwise direction the angle is +ve and if you rotate into a clockwise direction the angle is negative.

Remember as well that one complete revolution is 2 ? , thus the positive x-axis can correspond to either an angle of 0 or 2 ? (or 4 ? , or 6 ? , or -2 ? , or -4 ? , etc. based on the direction of rotation). Similarly, the angle ? /6 given angles: (to pick an angle totally at random) can also be any of the

? /6  +2 ? = 13 ?/6  (start at ? /6  then rotate once around counter clockwise)

? /6  + 4 ? = 25 ?/6  (start at ?/6  then rotate around twice counter clockwise)

? /6  -2 ?=11 ?/6 (start at ?/6      then rotate once around clockwise)

? /6  - 4 ? = 23 ?/6   (start at ?/6 then rotate around twice clockwise)

etc.

Actually ?/6 can be any of the given angles  ?/6 + 2 ? n , n = 0, ±1, ± 2, ±  3,.. In this case n refer to the number of complete revolutions you make around the unit circle begining at 6  .  Positive values of n correspond to counter clockwise rotations & -ve values of n correspond to clockwise rotations.

If you know the first quadrant then you can easily get all the other quadrants from the first along with a small application of geometry.