Two circles C(O, r) and C¹(O¹, r¹) touch each other at P, externally or internally. 

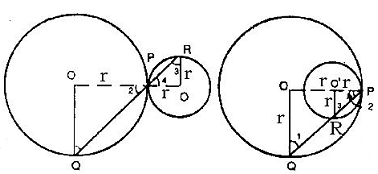
Construction: join OP and O¹P .
Proof : we know that if two circles touch
each other, the point of contact lies on the line through the centres.
O, P,O¹ are collinear
OPO¹ is a sttraight line.
Case I: C(o,r) and C¹(o¹,r¹ )touch externally at P.
In ΔOPQ, OP=OQ= r
∠OQP =∠OQP (Angle opposite to equal sides)

Similarly in ΔO¹PR, O^|P= O^|R=r^|

∠ORP = ∠RPO -------(2)

Also ∠OPQ = ∠RPO -------(3) (Vertically opposite angles)

From (1),(2) and(3) we get
∠OQP = ∠RPO

But these are alternate angles
=> OP u O1R
Case I I: C(o,r) and C(o¹,r¹) touch internally at P .
In ΔOPQ, OP=OQ= r

∠OQR = ∠O^|RP ...................(4) (angles opposite to equal side)

Similirarly in ΔO^|PR, O^|P = O^|R =r^|

 ∠ORP = ∠O¹PR ...................(5)

From (4) and (5) we get ∠OQR = ∠O^|RP

But these are correspondingg angles.

OQ // O^|R