Trivial Rejection Case of cohen sutherland line clippings

Case: it  is Trivial Rejection Case; if the logical intersection (AND) of the bit codes of the end points P, Q of the line segment is ≠ 0000 then line segment is not observable or is rejected.

Notice that, in figure of various cases of Cohen Sutherland Line Clippings, line 2 is totally on the top of the window but line 3 is neither on top nor at the in bottom plus, either on the left hand side nor on the right hand side of the window. We utilize the standard formula of logical ANDing to test the non visibility of the line segment.

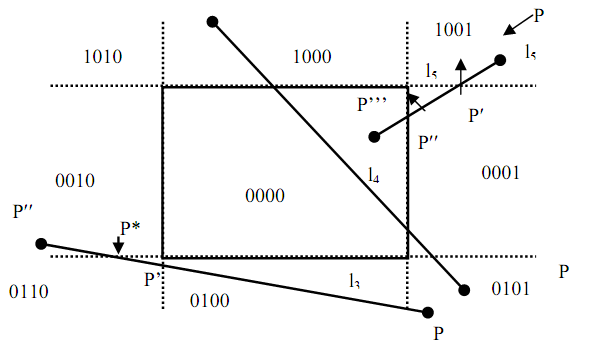
Figure: Cohen Sutherland line clipping

 Consequently, to test the visibility of line 2 and 3 we require calculating the logical intersection of end points for line 2 and lining 3.

Line l2: bit code of end points are 1010 and 1000 logical intersection of end points = (1010) ^ (1000) = 1000 like logical intersection ≠ 0000. Hence line 2 will be invisible.

Line l3: end points have bit codes 0010 and 0101 here logical intersection = 0000, that is, 0010 ^ 0101 = 0000 from the Figure of various cases of Cohen Sutherland Line Clippings, the line is invisible. Likewise in line 4 one end point is on top and another on the bottom therefore, logical intersection is 0000 although then it is partially visible, similar is true along with line 5. Such are exact cases and we will illustrate them in case 3.