Trig Functions: The intent of this section is introducing you of some of the more important (from a Calculus view point...) topics from a trig class.  One of the most significant (but not the first) of these topics will be how to employ the unit circle.  We will in fact leave the most significant topic to the next section.

First let's begin with the six trig functions and how they associate to each other.

cos ( x )                                             sin ( x )

tan ( x ) = sin ( x ) /cos ( x )               cot ( x ) = cos ( x ) /sin ( x ) =1/tan ( x )

sec ( x )= 1/ cos ( x )                         csc ( x ) = 1/sin ( x )

Recall that all the trig functions can be described in terms of a right triangle.

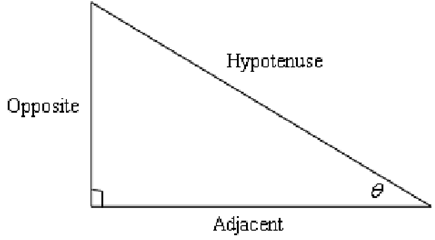
From this right triangle we get the given definitions of the six trig functions.

Cos θ = adjacent /hypotenuse sin θ = opposite/ hypotenuse

tan θ = opposite / adjacent      cot θ = adjacent /opposite

sec θ = hypotenuse /adjacent  csc θ∏ = hypotenuse /opposite

Remembering both the relationship among all six of the trig functions and their right triangle definitions will be useful in this course on occasion.

Next, we have to touch on radians. Mostly it is done in the terms of degree. The simialr is true in many science classes.  Though, in a calculus almost everything is done in radians. The given table gives some of the basic angles in both degrees & radians.

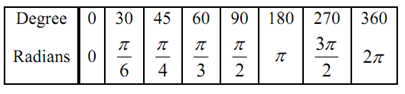
We might not see these particular angles all that much while we get into the Calculus portion of these notes, but knowing these can help us to visualize each angle.  Now, one more time just ensure this is clear.

Be forewarned, everything in mostly calculus will be done in radians!