Transverse Wave Stretched String

As a typical example of wave motion in one-dimension, let us consider the transverse harmonic waves on a long, taut string. We assume that in equilibrium position, the string is horizontal (along X-axis) under sufficient tension T so that we can neglect the effect of gravity.

If the string is sufficiently long, it is possible to set up of a harmonic wave moving in one direction on it by making transverse SHM of one of its free ends, at x = 0. (The other end is too far off so that we are not immediately concerned whether it is free or fixed.)

We look at a small portion AB of length δ x which is displaced in the vertical plane by a small amount from its equilibrium position. In the displaced position of the string, the tensions on the part AB are T (x) and T (x + δ x), as shown in fig. acting tangentially to the string at points A and B. Neglecting gravity, the vertical and horizontal components of resultant force onAB are

F_v = T (x + δx) sin (θ + δ θ) - T (x) sin θ

and, F_H = T (x + δx) cos (θ + δ θ) - T (x) cos θ

For small displacements, we assume that tension in the string does not vary appreciably from point to point, so that T (x + δx) ? T (x) = T. Further, small displacement implies that angles θ etc. are small so that we approximately put

sin (θ + δ θ) ? tan (θ + δ θ)     and sin θ ? tan θ

cos (θ + δ θ) ? cos (θ) ? 1

Hence, we get F_H = 0

and, F_v = T(tan (θ + δ θ) - tan θ) = T δ (tan θ)

Since tan θ = ∂y/∂x , where y denotes the displacement along vertical direction, we have

 

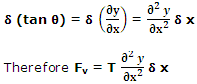
where m is the mass of the portion AB of string. If we write    as the mass per unit length of the string, we have m =    δ x. Hence, we get

 

That is, the equation of motion for the small piece of string is a wave equation of the type, where the wave velocity is given by

 

The wave velocity depends only on the characteristics of string, i.e. its mass per unit length    and tension T. All kinds of disturbances travel with the same velocity v, for a given    and T. Hence, if we move one end of the string up and down inSHM of amplitude A and frequency v, the disturbance moves along the string as a travelling harmonic wave given by

y (x, t) = A sin (2 π)/λ (x - vt)

where wavelength λ = v/v'.

If we vibrate the x = 0 end of the string between time t = t₁ to t = t₂ and then stop, then there would appear on the string a train of sine (or cosine) waves of limited extent, contained at any instant, between x = x₁ to x = x₂ such that

x₂ - x₁ = v (t₂ - t₁)

We call such a limited disturbance as a wave train which contains (x₂ - x₁)/λ number of waves, corresponding to (t₂ - t₁)/Toscillations performed at x = 0 end. On the other hand, if there is continuous vibration of free end, we get a continuous stream of waves. Note that in general a disturbance may be a continuous pattern, a finite wave train, or just a brief pulse.