Translation - 2-d and 3-d Transformations

It is the process of changing the position of an object. Suppose an object point P(x,y)=xI+yJ be moved to P'(x',y') by the specified translation vector V= t_xI + t_yJ; here t_x and t_y is the translation factor in x and y directions, hence

P'=P+V.                                 ----------------(1)

In element form, we have:

Tv=        x'=x+ t_x   and

y'=y+t_y                      ----------------(2)

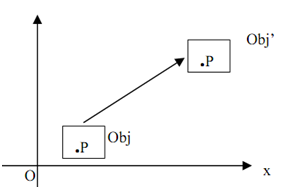
As demonstrated in Figure 2, P' is the new location of P, after moving t_x along x-axis and t_y along y-axis. This is impossible to enlarge a relation of the form.

P'=P.T_v                                                        ---------------(3)

Here T_v is the transformation for translation in matrix form.

We cannot present the translation transformation in (2x2) matrix form as 2-Dimentional Euclidean system.

Any transformation operation can be shown as a (2x2) matrix form, but except translation, which is translation transformation cannot be expressed like a (2x2) matrix form 2-Dimentional Euclidean system. Although via using Homogeneous coordinate system i.e. HCS, we can show translation transformation in matrix form. The Homogeneous coordinate system and advantages of by using Homogeneous coordinate system is discussed, in brief detail, in section of homogeneous coordinate systems.