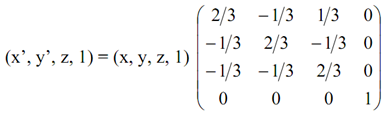Transformation for Isometric projection - Transformation
Suppose that P(x,y,z) be any point in a space. Assume as a given point P(x,y,z) is projected to the P'(x'y',z') on the projection plane as x + y + z = 0. We are involved to determine the projection point P'(x',y',z').
The parametric equation of a line passing via point P(x, y, z) and towards d (1, 1, 1) is:
P + t.d = (x, y, z) + t. (1,1,1) = (x + t, y + t, z + t) is any one point of on the line, here - ∞< t < ∞. The point P' can be acquired, whereas t = t*.
Hence P'=(x',y',z')=(x + t*,y + t*,z + t*), as P' lies on x + y + z = 0 plane.
ð (x + t*)+(y + t*) + (z + t*)=0
ð 3.t*=-(x + y + z)
ð t*=-(x + y + z)/3 must be true.
ð x'= (2.x - y - z)/3 , y'=(-x +2.y - z)/3 , z'=(- x - y +2.z)/3
Hence, P'=(x',y',z')=[(2.x -y-z)/3, (-x +2.y- z)/3, (-x-y+2.z)/3]
In terms of homogeneous coordinates, we acquire: