A freight train from Melbourne is approaching Sydney, carrying n cars of cargos. The cargos are to be delivered to n different cities in the metropolitan area of Sydney - one car for one city. To avoid delays of stoping at each city station, the train is to dismiss a car once the car arrives its destination station without unloading the car, providing the car was at the end of the train. Since all these cars of the train were collected on the way from Melbourne to Sydney, the order of these cars does not match the order of their designations. The train have to be reorganised in the Railway Switching Junction outside Sydney to reorder its cars to match the order of their destinations (See Figure). The aim of this assignment is to design and implement an algorithm to simulate the procedure of car re-ordering.
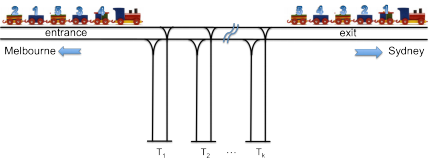
The above figure shows the diagram of the railway switching junction. The junction has a single entrance and a single exit on the main railway from Melbourne to Sydney. There are k transit rails, denoted by T1, T2, ..., and Tk, linked to the main railway for a train to transfer cars. The train can drive in or out each transit rail either forward or backward.
The train can be disconnected at any point between two cars. A car can be parked in a transit rail but cannot be left on the main track. A car cannot move without connecting to the engine (only one engine). We assume that the transit rails and their distance in between are long enough for the train to drive in and out in full length.
Assume that the destination stations in Sydney are labelled from 1 to n, arriving Station n first and ending at Station 1. Each car of the train is marked in accord with its destination.
When the train arrives, the order of the cars from the engine to the last car is c1,c2,...,cn, which can be any permutation of the numbers 1,2,...,n. As an example shown in Figure 1, when the train arrives the junction, the order of the cars is 4,3,5,1,2. The cars need to be re-ordered into 1,2,3,4,5 to be delivered at their destination stations.