Thrust diagrams for the beam:

Illustrate the shear force, bending moment & thrust diagrams for the beam illustrated in Figure

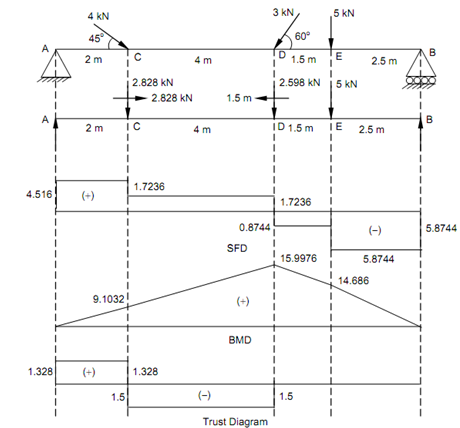
Figure

Solution

Vertical component of 4 kN at C, = 4 × sin 45^o = 2.828 kN ( ↓ )

 Horizontal component of 4 kN at C, = 4 × cos 45^o = 2.828 kN ( → )

Vertical component of 3 kN at D, = 3 × sin 60^o = 2.598 kN ( ↓ )

Horizontal component of 3 kN at D, = 3 × cos 60^o = 1.5 kN ( ← )

Taking moments around B,

R_B  × 10 - 5 × 7.5 - 2.598 × 6 - 2.828 × 2 = 0

R_B  = 5.8744 kN

R_A  = 2.828 + 2.598 + 5 - R_B  = 10.426 - 5.8744

R_A  = 4.5516 kN

Shear Force (Beginning from the Left End A)

SF at A, F_A  =+ 4.5516 kN

SF just left of C, F_C  =+ 4.5516 kN

SF just right of C, F_C  =+ 4.5516 - 2.828 =+ 1.7236 kN

SF just left of D, F_D  =+ 1.7236 kN

SF just right of D, F_D  = + 1.7236 - 2.598 = - 0.7844 kN

SF just left of E, F_E  =- 0.8744 kN

SF just right of E, F_E  =- 0.8744 - 5 =- 5.8447 kN = Reaction at B.

Bending Moment (Beginning from the Right End B)

BM at A and B,          M_A = M_B = 0

 BM at E, M _E  = + (5.8744 × 2.5) = + 14.686 kN-m

BM at D, M _D  = + 5.8744 × 4 - 5 × 1.5 = + 15.9976 kN-m

BM at C, M _C  = + (4.5516 × 2) = + 9.1032 kN-m  (considering left side)

Maximum Bending Moment

It shall occur at D where SF changes sign.

Thus, M _max  = + 15.9976 kN-m

Thrust Diagram

 Let us find out the horizontal reaction at A (being a hinged end).

∑ H = 0

+ H _A - 2.828 + 1.5 = 0

∴          H _A = 1.328 kN

The section AC is subjected to 1.328 kN (tensile force).

The section CD is subjected to 1.5 kN (compressive force).

∴          (2.828 - 1.328 = 1.5)