THINKING MATHEMATICALLY :  Have you ever thought of what mental processes you are going through when you are solving a mathematical problem? Why don't you try the following problem?

While doing it, carefully monitor the mathematical processes you are undergoing. The problem is to find out what the relationship is between the arithmetic mean (AM) and the geometric mean (GM) of any two positive numbers.

How would you tackle this? Would you start by looking at a few specific pairs of numbers? If so, you are specialising.

Now, suppose you take, say 1 and 3. The AM of 1 and 3 is(1+3)/2 The GM of 1 and 3 is √1×3 = √3. By taking several pairs, suppose you get the following chart: √3

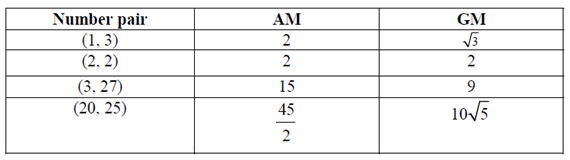
Do you start noticing a pattern? Does this make you conjecture a rule? What is the general rule? Is it that AM ≥GM? You need to check if your generalisation is right. This means that you need to prove your conjecture. This means that you need to start from certain assumptions, and arrive at your result by a series of steps, each following logically from the previous one.

There are several ways of proving it. One way is that you can take any two positive numbers x and y. Now, you want to see whether

X+y/2≥√xy

This wills he true if and only if

Learning algorithms is not learning mathematics.

For positive numbers m and n, their AM is

 (x + y) ≥ 2 √xy , which is true if and only if

(x + y)² ≥ 4xy , which is true if and only if

x² + y² + 2xy ≥ 4xy , which is true if and only if

x² + y² - 2xy ≥ 0 , which is true if and Only if

(x - y)² ≥ 0 , and this is always true, since the square of a number is always non-negative.

So, you have proved the general rule that the AM of any two positive numbers is greater than or equal to their GM.

But, may be your curiosity has been provoked. Are you wondering if a similar statement is true for 3 positive numbers? Or for negative numbers? In this case, you are posing a problem. Of course, once you pose it, I'm sure you'll test your conjecture, and prove or disprove it. And, carrying on in this manner, you may generalise your statement to n numbers, and prove it.

Remember that, without a proof your conjecture is not acceptable as a true mathematical statement.

Sometimes, of course, you may make a conjecture which is not right. For example, suppose that you had initially found the values of the AM and GM for the pairs (1,1), (2,2), (3,3), and so on. Then you could have conjectured that AM = GM. But then, to test this, you may have tried it out for (1,3), and discovered that your conjecture isn't correct. So, you would need to modify it, and then develop your mathematical argument again.

So, what have you been doing in the process of problem-posing and problem solving?

Weren't you thinking mathematically along the following lines?

E1) Several circles can be drawn through a point. How many can be drawn through two points, or three points,...?

a) Work on this problem and note down the processes you use.

b) Did the properties of mathematics, show up while you were developing your arguments? If so, in what way?

If you've done, you must have realised that trying mathematical problems improves one's abilities to

• think precisely
• articulate clearly
• think logically and systematically
• look for patterns and relationships

These abilities, if well developed, can help us greatly in other real-life situations. Therefore, these mental abilities should be developed right from childhood on.