Q. Thermodynamics of Reduction Process?

As you have read above, metallurgy of most metals involves reduction of their oxides. The nature of the reduction process depends upon the ease which the oxide can be reduced. Some ox- so easily reduced that they decompose just by heating at relatively low temperatures. For example, Priestley, in his experiments on oxygen produced metallic mercury and oxygen from mercuric oxide by simply heating it with sun light. When sun light as focused on Hg O by means of a magnifying glass, it decomposed spontaneously according to the equation:

2HgO(s) ------------> 2Hg (g) + O₂ (g)

The practicality of producing a free metal by thermal decomposition depends on the extent to which the reaction proceeds to completion at a given temperature. As you know, the feasibility of the reaction is governed by the free energy change taking place during the reaction. When AGO for a reaction is negative, the reaction is feasible from a practical stand point because significant amounts of products will be formed. You know that the standard free energy change, AG O, is related to the standard enthalpy change, W , and the standard entropy change, AS" , according to the following equation:

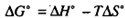
In other words, the sign and magnitudes of AV anΔ AS" control the sign and magnitude of ΔG'. Let us look little deeper into this relationship.

Since in the decomposition of an oxide, oxygen is produced in the gaseous form and sometimes the metal may also be produced in vapour form, the process occurs with a sizeable increase in entropy, so ΔS will be positive. Enthalpy of decomposition, ΔH^oΔ- is simply the negative of the enthalpy of formation of the oxide, ΔH^e_f since ΔH^e_f is generally negative for metal oxides, enthalpy of decomposition will be positive. As a result, the sign of ΔG" is determined by the difference between two positive quantities ΔH^o anΔ TΔS^o T the absolute temperature being always positive.

From the above, we can deduce that if the enthalpy of formation of the metal oxide is small

as in case of HgO, Ag₂0, CuO anΔ Au₂0₃, then the enthalpy of decomposition will be a small positive quantity anΔ ΔG^O , which is given by the difference of ΔH⁰ anΔ TΔS₀ , will become negative at relatively low temperatures. These oxides are said to have relatively low the bal stabilities. On the other hand, if the oxide has a large negative enthalpy of formation, then the enthalpy of decomposition of the oxide will be a large positive quantity. As a result, the value of ΔG^O will become negative at a very high temperature where TΔ so becomes larger than ΔH⁰. Thus, the metal oxiΔe woulΔ be stable with respect to thermal Δecomposition. In order to decompose such a metal oxide, it would have to be heated to a very high temperature at which cost becomes prohibitive. Thus, a knowledge of how the standard free energy change, ΔG^O, for the reduction reaction varies with temperature is very important.