The median
- it is a statistical value which is usually located at the center of a given set of data that has been organized in the order of size or magnitude as illustrating, consider the set 14, 17, 9, 8, 20, 32, 18, 14.5, 13. While the data is ordered it will be 8, 9, 13, 14, 14.5, 17, 18, 20, 32
The middle number or median is 14.5
- The significance of the median lies in the fact that it divides the data into two equivalent halves. The number of observations above and below the median is equal.
- In order to find out the value of the median from grouped data. While data is grouped the median may be determined by utilizing the given methods.
i. Graphical method by using the cumulative frequency curve or ogive
ii. The formula
Illustration
Referring to the table which is given below; determine the median by using the methods above
|
IQ
|
No of resid
|
UCB
|
Cumulative Frequency
|
|
0 - 20
|
6
|
20
|
6
|
|
20 - 40
|
18
|
40
|
24
|
|
40 - 60
|
32
|
60
|
56
|
|
60 - 80
|
48
|
80
|
104
|
|
80 - 100
|
27
|
100
|
131
|
|
100 - 120
|
13
|
120
|
144
|
|
120 - 140
|
2
|
140
|
146
|
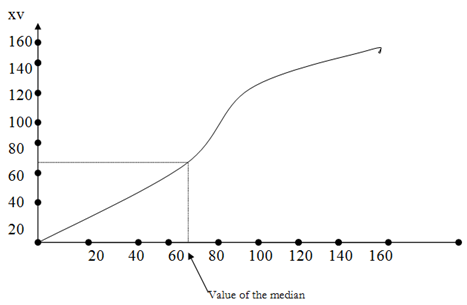
Hence the position of the median is= (n + 1)/2
= (146 + 1)/2
ii. Computation
The formula utilized is
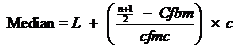
Whereas L = Lower class boundary of the class having the median
N = No of observations
Cfo= cfbm = Cumulative frequency of the class before that having the median
F1 fmc = Frequency of the class having the median
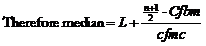
= 60 + ((73.5 - 56)/48) * 20
= 60 + 7.29
= 67.29