The Definition of the Limit

In this section we will look at the precise, mathematical definition of three types of limits we'll be looking at the precise definition of limits at finite points which have finite values, limits which are infinity & limits at infinity.  We'll also give the accurate, mathematical definition of continuity.

Let's begin this section out with the definition of a limit at a finite point which has a finite value.

Definition 1 

Let f(x) be a function described on an interval which contains x = a , except possibly at x = a .  Then we say that,

If for each number ε > 0 there is some number δ > 0 such that

|f ( x ) - L | < ε             whenever       0 < |x - a| < δ

That's mouth full. Now that it's written down, just what does it mean?

Let's take a look at the given graph and let's also suppose that the limit does exist.

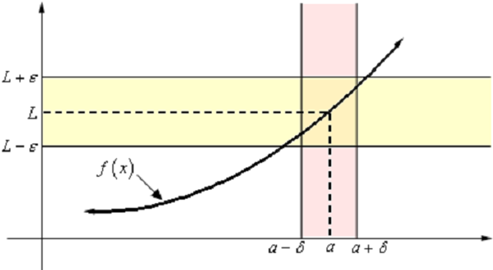
What the definition is saying us is that for any number ε > 0 which we pick we can go to our graph and sketch two horizontal lines at L + ε and L - ε as illustrated onto the graph above. Then somewhere out there in the world is another number δ > 0, that we will have to determine, which will let us to add in two vertical lines to our graph at a + δ & a - δ .

Now, if we will take any x in the pink region, i.e. between a + δ and a - δ , then this x will be near to a than either of a + δ and a - δ

                                                   |x - a| < δ

If now we identify the point on the graph which our choice of x gives then this point on the graph will lie in the intersection of the pink and yellow region.  It means that this function value f(x) will be near to L than either of L + ε & L - ε .  Or,

                                                        |f ( x ) - L | < ε

Thus, if we take a value of x in the pink region then the graph for those values of x will lie between the yellow region.

Notice as well that there are in fact an infinite number of possible δ 's that we can select.  Actually, if we go back & look at the graph above this looks like we could have taken a slightly larger δ and yet gotten the graph from that pink region to be totally contained in the yellow region.

Also, notice as well that as the definition points out we only have to ensure that the function is described in some interval around x = a however we don't really care if it is defined at x = a . Recall that limits do not care about what is happening at the point; they only care  about what is happening about the point in question.

Now that we've the definition out of the way & made try to understand it let's illustrates how it's in fact used in practice.

These are a little difficult sometimes and it can take many practice to obtain good at these so don't feel too bad if you don't pick on this stuff right away.  We will look at a couple of examples that work out fairly easily.