Arithmetic mean
Arithmetic means is commonly known as average or mean it is acquired by first of all summing up the values provided and by dividing the total value by the total no. of observations.
That is mean = ( ΣX)/n
Whereas x = no. of values
∑ = summation
n = no of observations
Illustration
The mean of 60, 80, 90, 120
(60 + 80 + 90 + 120)/4
= 350/4
= 87.5
The arithmetic mean is extremely useful since it represents the values of most observations in the population.
Therefore the mean describes the population rather well in terms of the magnitudes attained by most of the members of the population
Computation of the mean from grouped Data that is in classes.
The given data was acquired from the manufacturers of electronic cells. A sample of electronic cells was taking and the life spans were recorded as displayed in the given table:
|
Life span hrs
|
No. of cells (f)
|
Class MP(x)
|
X - A = d
|
fd
|
|
1600 - 1799
|
25
|
1699.5
|
-600
|
-15000
|
|
1800 - 1999
|
32
|
1899.5
|
-400
|
-12800
|
|
2000-2199
|
46
|
2099.5
|
-200
|
-9200
|
|
2200 - 2399
|
58
|
2299.5(A)
|
0
|
0
|
|
2400 - 2599
|
40
|
2499.5
|
200
|
8000
|
|
2600 - 2799
|
30
|
2699.5
|
400
|
12000
|
|
2800 - 2999
|
7
|
2899.5
|
600
|
4200
|
A = Assumed mean that this is an arbitrary number chosen from the data, MP = mid point
Arithmetic means = Assumed mean +(åfd)/(f)
2299.5 + (-((12800)/238))
= 2299.5 +(-53.78)
2245.72 hours
Illustration 2
Employ of the coded method The given data was acquired from students who were registered in a specific college.
The table displays the age distribution:
|
Age (yrs)
|
No. of Students (f)
|
mid points (x)
|
x-a = d
|
D/c = u
|
fu
|
|
15 - 19
|
21
|
17
|
-15
|
-3
|
-63
|
|
20 - 24
|
35
|
22
|
-10
|
-2
|
-70
|
|
25 - 29
|
38
|
27
|
-5
|
-1
|
-38
|
|
30 - 34
|
49
|
32(A)
|
0
|
0
|
0
|
|
35 - 39
|
31
|
37
|
+5
|
+
|
31
|
|
40 - 44
|
19
|
42
|
+10
|
+2
|
38
|
|
|
193
|
|
|
|
-102
|
Required compute the mean age of the students by using the coded method
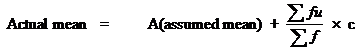
= 32 + ((-102)/193) * 5
= 29.36 years