Taylor Series - Sequences and Series
In the preceding section we started looking at writing down a power series presentation of a function. The difficulty with the approach in that part is that everything came down to requiring to be able to relate the function in some way to
1/(1-x)
and when there are many functions out there that can be related to this function there are so many that simply can't be related to this.
Thus, without taking anything away from the procedures we looked at in the preceding section, what we require to do is come up with a much more general method for writing a power series presentation for a function.
Thus, for the time being, let us make two assumptions. First, let's suppose that the function f (x) does in fact have a power series presentation about x = a,
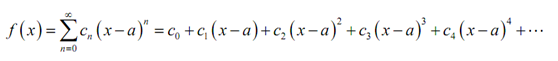
Next, we will need to assume that the function, f (x), has derivatives of every order and that we can in fact find them all.
Now here that we've assumed that a power series representation available we need to determine what the coefficients, cn are. This is easier as compared to it might at first appear to be. Let us first just evaluate everything at x = a. This specifies,
f (a) = C0
Thus, all the terms apart from the first are zero and we now know what c0 is. Not fortunately, there is not any other value of x that we can plug into the function that will permit us to rapidly find any of the other coefficients. Though, if we take the derivative of the function (and its power series) after that plug in x = a we obtain,
f' (x) = c1 + 2c2 (x-a) + 3c3 (x-a)2 + 4c4 (x-a)3 + .....
f'(a) = c1
and we now recognize c1.
Let us carry on with this plan and find out the second derivative.
f'' (x) = 2c2 + 3(2) c3 (x-a) + 4 (3) c4 (x-a)2 + ....
f'' (a) = 2c2
Thus, it looks like,
C2 = f'' (a) / 2
By using the third derivative gives,
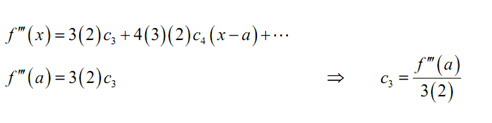
By using the fourth derivative gives,
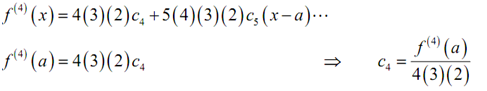
With anticipation by this time you have seen the pattern here. Generally it looks like, we've got the subsequent formula for the coefficients.
Cn = f(n)(a) / n!