Linear Systems with Two Variables

A linear system of two equations along with two variables is any system which can be written in the form.

                           ax +by = p

                          cx +dy = q

Where  value of any of the constants can be zero  along with the exception which each equation ought to  have at least one variable in it.

Also, the system is known as linear if the variables are just to the first power, are only in the numerator & there are no products of variables in any of the equations.

Following is an example of a system with numbers.

3x - y = 7

2x + 3 y = 1

Before we discuss how to solve out systems we have to first talk regarding just what a solution to a system of equations is.  A solution to system of equations is value of x & a value of y that, while substituted into the equations, satisfies both of the equations at the similar time.

For the above example check  x = 2 and y = -1 is a solution to the system.  It is easy enough to

3( 2) - ( -1) = 7

2 ( 2) + 3( -1) =1

Thus, sure sufficient that pair of numbers is solution to the system.  Do not worry regarding how we got these values. It will be the extremely first system that we solve while we get into examples.

Note that it is significant that the pair of numbers satisfy both of the equations.  For example

x = 1 and y = -4 will satisfy the first equation, although not the second & so isn't a solution to the system.

Similarly x = -1 and y =1 will satisfy the second equation however not the first and thus can't be solution to the system.

Now, only what does a solution to a system of two equations represent? Well if you think regarding it both of the equations in the system are lines.  Thus, let's graph them and see what we get.

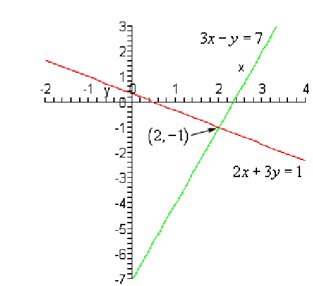
As you can illustrate the solution to the system is the coordinates of the point where intersect the two lines.  thus, when solving linear systems along two variables we are really asking where the two lines will intersect.