Symmetric Central Force
A central force is spherically if the magnitude of the force does not depend on the direction (angles θ, or Ø) of the particle but only on distance r from the center of the force, that is F is spherically symmetric if,
F = F ( r ) er
A spherically symmetric force is conservative, conversely, if a central force F during a small displacement d l of the particle:
dW = F . d l = ( F ( r ) er ) . ( er dr + eθ r dθ)
= F ( r ) dr
where we used dl in polar co-ordinates. The work done in moving the particle from r1 to r2, therefore, is
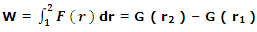
where, G ( r ) is the integral function of F ( r ); that is, F ( r ) = dG ( r )/dr
The work done thus depends only on the end co-ordinates and not on the path followed. Force F ( r ) er is therefore conservative.
G ( r ), in fact expresses the negative of potential energy function U ( r ):
W = - ( U ( r2 ) - U ( r1 ))
For example, the gravitational and electrostatic forces are spherically symmetric central forces. These are expressed as
.png)
We discussed these forces earlier; the potential energy of interaction for the two particles in case of above forces is:
.png)
The central forces (like gravitational or electrostatic) which vary as (1/r2) are called inverse square forces.
The conservation of energy principal for a particle moving in a spherically symmetric central force is expressed as,
½ mv2 + U ( r ) = E , constant
.png)
On the other hand, the angular momentum of the particle is also a constant of motion:
.png)
Hence we get
.png)
.png)
represents an effective potential energy. (Remember, L2/2 mr2 is really a part of kinetic energy coming from transverse motion of the particle.)
If the particle motion is a one-dimensional motion along the radial direction under effective potential energy function U' ( r ). The entire effect of transverse motion of the particle is incorporated in the potential energy as additional L2/2 mr2 term.
The term L2/2mr2 is sometimes referred to as the 'centrifugal' potential energy. This is because the corresponding force is,
.png)
which is same as centrifugal force mr ω2 in a co-ordinate frame rotating with instantaneous angular velocity ω = dθ/dt.