SUMMATION NOTATION

Under this section we require to do a brief review of summation notation or sigma notation.  We will start out with two integers, n and m, along with n < m and a list of numbers denoted as given here,

a_n, a_n+1, a_n+2,..............,a_m-2, a_m-1, a_m

We need to add them up, or say as,

a_n + a_n+1 + a_n+2+...........+a_m-2 + a_m-1 + a_m

For large lists it can be a fairly cumbersome notation therefore we establish summation notation to denote these types of sums. The case above is denoted as given here.

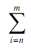a_I = a_n + a_n+1 + a_n+2+...........+a_m-2 + a_m-1 + a_m

The i is termed as the index of summation. This notation gives us to add all the a_i's up for all integers starting at n and ending on m.

 For illustration,

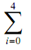i/(i+1) = (0/(0 +1)) + (1/(1 + 1)) + (2/(2 + 1)) + (3/(3 + 1)) + (4/(4 + 1)) = 163/60 = 2.71667¯

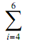2ⁱ x2ⁱ⁺¹ = 2⁴ x⁹ + 2⁵ x¹¹ + 2⁶ x¹³ = 16 x⁹ + 32 x¹¹ + 64 x¹³

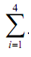f(x_i*) = f(x₁*) + f(x₂*) + f(x₃*) = f(x₄*)