We know that the terms in G.P. are:
a, ar, ar2, ar3, ar4, ................, arn-1
Let s be the sum of these terms, then
s = a + ar + ar2 + ar3 + ar4 + ................+ arn-1
or
|
s
|
= |
 |
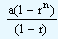This is obtained as follows:
We know that
s = a + ar + ar2 + ar3 + ar4 +.............+ arn - 1 ......(1)
Multiplying this with "r" throughout, we have
r.s = r.a + r.ar + r.ar2 + r.ar3 + r.ar4 +........+ r.arn-1
= ar + ar2 + ar3 + ar4 + ar5 +.......+ arn ......(2)
Subtracting (1) from (2), we have
r.s - s = (ar - a) + (ar2 - ar) + (ar3 - ar2) +.......+ (arn - arn-1)
After canceling the terms equal in magnitude but opposite in sign, we are left with
| s(r - 1) |
= |
arn - a |
| s(r - 1) |
= |
a(rn - 1) |
| or s |
= |
 |
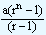By changing the signs in the numerator and the denominator we can also write the above equation as
| s |
= |
|
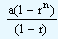What happens to the above formula if the value of n is very large. The above formula can be written as
|
s
|
= |
 |
|
|
As the value of n approaches infinity (very large) the expression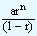 
becomes smaller to that extent where we ignore it. In this case the nth term is given as
|
Tn
|
= |
 |
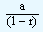Now we look at a couple of examples.
Example
Find the sum of the series which is given below to 13 terms.
81, 54, 36, .............
The first term 'a' = 81 and the common ratio is obtained from the ratio of 54 and 81 or 36 and 54. It is 54/81 = 2/3. Now we employ the formula given above to calculate the sum of series to 13 terms.
| s |
= |
|
|
 |
|
|
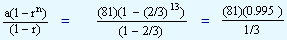= 241.78
The same series if considered as an infinite series, the sum of n terms would be
| T |
= |
 |
|
|
= |
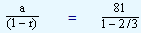243 |