Q. Draw  the structures of complete  undirected  graphs  on  one,  two,  three,  four  and  five vertices also prove that the number of edges in an n vertex complete graph is n(n-1)/2.         

Ans:

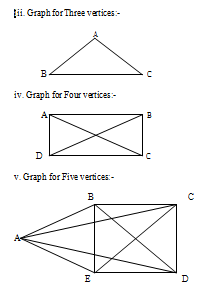
The Graphs are drawn below:

i. Graph for One vertex:-

.A

ii. Graph for Two vertices:-

From the above drawn Graphs we can see

i.     When n=1,

Then number of edges becomes

=n(n-1)/2

= 1(1-1)/2

=1(0)/2

=0/2

=0

Therefore, number of edges = 0. ii.   When n=2,

Then number of edges becomes

=n(n-1)/2

=2(2-1)/2

=2(1)/2

=2/2

=1

Therefore, number of edges = 1. iii. When n=3,

Then number of edges becomes

=n(n-1)/2

=3(3-1)/2

=3(2)/2

=6/2

=3

Therefore, number of edges becomes = 3.
 iv.   When n=4,

Then number of edges

=n(n-1)/2

=4(4-1)/2

=4(3)/2

=12/2

=6

Therefore, number of edges becomes = 6.
 v. When n=5,

Then number of edges becomes

=n(n-1)/2

=5(5-1)/2

=5(4)/2

=20/2

=10

Therefore, number of edges becomes = 10.