Before going to solving differential equations we must see one more function. Without Laplace transforms this would be much more hard to solve differential equations which involve this function into g(t).

The function is the Heaviside function and is described as,

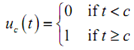
Now there is a graph of the Heaviside function.

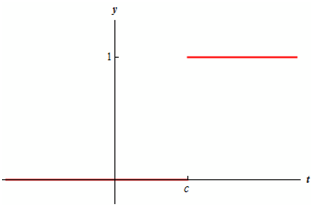
Heaviside functions are frequently termed as step functions. Now there is some optional notation for Heaviside functions.

u_c (t) = u (t - c ) = H (t - c)

We can consider of the Heaviside function like a switch that is off till t = c at that point it turns on and contains a value of 1. Therefore what if we need a switch which will turn on and gets some other value, as 4, or -7?

Heaviside functions can merely take values of 0 or 1, although we can use them to find other types of switches. For illustration 4u_c(t) is a switch which is off until t = c and then turns on and gets a value of 4.  Similarly, -7u_c(t) will be a switch which will acquire a value of -7 when it turns on.

Now, suppose that we want a switch that is on (with a value of 1) and then turns off at t = c. We can use Heaviside functions to represent it suitably. The subsequent function will exhibit this type of behavior.

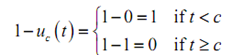
Proceeding to t = c the Heaviside is off and thus has a value of zero. The function as complete so for t < c has a value of 1.  As we hit t = c the Heaviside function will start and the function will now get a value of 0.

We can as well modify it so this has values other than 1 while it is one. For illustration,

3 = 3u_c(t)

It will be a switch which has a value of 3 till it turns off on t = c. We can use also Heaviside functions to present much more complicated switches.