Standard interpretations to derivatives

Example   Assume that the amount of money in a bank account is specified by

                                      P (t ) = 500 + 100 cos (t ) -150 sin (t )

where t refer to in years.  During the first 10 years in which the account is open while is the amount of money in the account increasing?

Solution: To find out when the amount of money is increasing we have to determine while the rate of change is positive.  As we know that the rate of change is specified by the derivative that is the first thing that we have to find.

                                         P′ (t) = -100 sin (t) -150 cos (t)

Now, we have to find out where in the first 10 years it will be positive. It is equivalent to asking where in the interval [0, 10] the derivative is positive.  Recall that both sine & cosine are continuous functions and hence the derivative is also continuous function. Then the Intermediate Value Theorem tells us that the derivative can only change sign if it first goes through zero.

Therefore, we ought to solve the following equation.

-100 sin (t) -150 cos (t) = 0

100 sin (t) = -150 cos (t)

sin (t ) /cos (t ) = -1.5

tan (t ) = -1.5

The solution to this equation is,

t = 2.1588 +2 ? n,                                n = 0, ±1, ±2,........

t = 5.3004 + 2 ? n,                               n = 0, ±1, ±2,......

If you don't recall how to solve out trig equations go back & take a look at the sections on solving out trig equations in the Review chapter.

Only we are interested in those solutions which fall in the range [0, 10].  Plugging in values of n into the solutions above we see that the values we require are,

t = 2.1588

t =5.3004            t =2.1588 +2 ? =8.4420

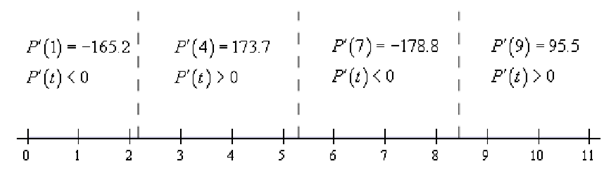
Thus, much like solving polynomial inequalities all that we have to do is sketch in a number line and adds in these points. These points will divide number line into regions where in the derivative have to always be the similar sign.  All that we have to do then is select a test point from each of the region to find out the sign of the derivative in that region.

Following is the number line along with all the information on it.

Thus, it looks as the amount of money in the bank account will be increasing at the time of following intervals.

2.1588 < t < 5.3004    8.4420 < t < 10

Note as well that we can't say anything about what is happening after t = 10 as we haven't done any work for t's after that point.