Spherical Coordinates - Three Dimensional Space

In this part we will introduce spherical coordinates. Spherical coordinates which can take a little getting employed to.  It's possibly easiest to start things off along with a diagram.

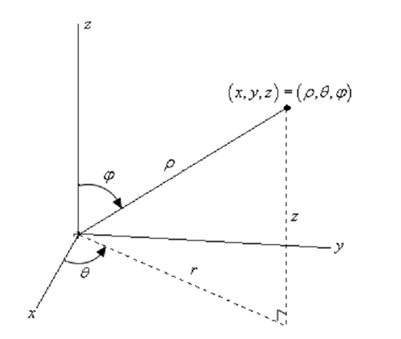
Spherical coordinates contains the following three quantities.

1^st there is ρ.  This is the distance from the origin to the point and we will need ρ ≥ 0 . After that there is θ.  This is similar angle that we saw in polar/cylindrical coordinates.  It is the angle in between the positive x-axis and the line above represented by r (that is as well the same r as in polar or cylindrical coordinates). There are not any type of restrictions on θ.

At last there is Φ.  This is the angle in between the positive z-axis and the line from the origin to the point. We will need 0 ≤ Φ ≤ Π.

In brief, ρ is the distance from the origin to the point, Φ is the angle which we require to rotate down from the positive z-axis to obtain to the point and θ is how much we require to rotate around the z-axis to get to the point.

We should first derive a few conversion formulas. Let's first start along with a point in spherical coordinates and ask over what the cylindrical coordinates of the point are. Thus, we know (ρ, θ, Φ)and wish to find ( r, θ, z).  Actually, we really only require to find r and z since θ is similar in both coordinate systems.

We will be capable to do all of our work by looking at the right triangle displayed above in our sketch. Along with a little geometry we see that the angle in between z and ρ is Φ and thus we can see that, z = ρ cos Φ

r = ρ sin Φ

and these are just the formulas that we were looking for. Thus, given a point in spherical coordinates the cylindrical coordinates of the point will be,

r = ρ sin Φ

θ = θ

z = ρ cos Φ

Notice: as well that,

Or,

r² + z² = ρ² cos² Φ + ρ² sin² Φ = ρ² (cos² Φ + sin² Φ) = ρ²

or

ρ² = r² + z²