Q. Define a sparse matrix. Explain different types of sparse matrices? Show how a triangular array is stored in memory. Evaluate the method to calculate address of any element ajk of a matrix stored in memory.                                                                                                                             

Ans.

Sparse Matrix

A m x n matrix A is said to be sparse if MOST of its elements are zero. A matrix that is not sparse is called dense matrix.

Types of Sparse matrix

1)            Diagonal Matrix

This is the square matrix where the non zero elements are only where row = col ie at

diagonal.

2)  Tridiagonal Matrix

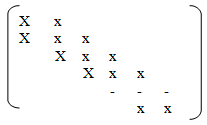
In  this  square  matrix  all  elements  other  than  those  on  and  on  the  diagonals immediately above and below this one are zero.

Triangular Matrices

Tiangular Matrices is of 2 types:

a)  Lower triangular b)  Upper triangular

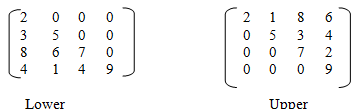
In an n*n lower triangular matrix A, row 1 has one non zero element, row 2 has 2,

....., and row n has n. whereas, in an n*n upper triangular matrix A, row 1 has n non zero elements, row 2 has n-1 ,.... , and row n has 1. In both the cases, the total number of non-zero elements is n(n+1)/2.

Both of these matrices can be represented using an one dimensional array la of size n(n+1)/2.

Consider lower triangular matrix L. the elements can be mapped by rows or by columns.

In a row-wise mapping, the element L[i,j], i>=j, is preceded by ∑k  for k=1 to i-1, elements that are in row 1 through i-1, and j-1 such elements from row i. the total number of elements that precede it in a row-wise mapping is

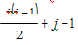
This expression also gives the position l[i,j] in la.

Method  to  calculate  address  of  any  element  ajk   of  a  matrix     stored  in memory.

Let us consider 2 dimensional array a of size m*n further consider that the lower bound for the row index is lbr and for column index is lbc.

Like linear array, system keeps track of the first element only i.e. , the base address of the array.

Using this base address, the computer computes the address of the element in the ith row and jth column i.e. loc(a[i][j]), using the following formulae:

Column major order:-

Loc (a[i][j]) = base (a) + w [m (j - lbc) + ( i - lbr)] in general

Row major order:-

Loc (a[i][j]) = base (a) + w [n(i - lbr) + ( j - lbc)]            in general

where w is number of bytes per storage location for any one element of the array.