Solving Trig Equations: Here we will discuss on solving trig equations. It is something which you will be asked to do on a fairly regular basis in my class.

Let's just see the examples to how to solve trig equations.

Example Solve 2 cos (t ) = √3 .

Solution

There's actually not a whole lot to do in solving this sort of trig equation.  All we have to do is divide both of the sides by 2 and the go to the unit circle.

2 cos (t ) =       √3

cos (t ) =          √3/2

hence, we are looking for all the values of t for which cosine will contain the value of √3/2 .  hence, let's take a look at the given unit circle.

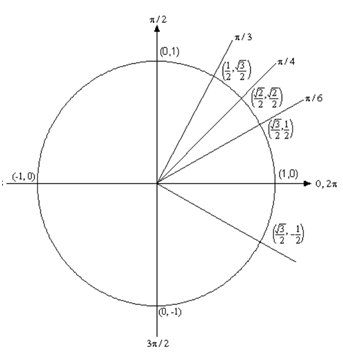
From quick inspection we can see that t = ?/6   is a solution.   There is another angle which will also be a solution.  We have to determine what this angle is. While we look for these angles typically we desire positive angles which lie between 0 and 2 ? . This angle will not be the just possibility certainly, however by convention typically we look for angles that meet these conditions.

To determine this angle for this problem all we have to do is use a little geometry.  The angle in the first quadrant makes an angle of ?/6 with the +ve x-axis, then hence must the angle in the fourth quadrant. Thus we could use - ?/6    , since again, it's more common to use positive angles thus, we'll use t = 2 ? - ?/6 = 11?/6

We aren't done along with this problem.  As the discussion regarding finding the second angle has illustrates there are several ways to write any given angle onto the unit circle.  Sometimes this will be - ?/6 that we desire for the solution & sometimes we will desire both (or neither) of the listed angles. Thus, as there isn't anything in this problem (contrast this along with the next problem) to tell us that is the correct solution we will have to list all possible solutions.

It is extremely easy to do.  Recall from the previous section and you'll illustrates there that I used

                                 ?/6  + 2 ? n  , n  =0, ± 1, ± 2, ± 3,.............

to show all the possible angles which can end at the similar location on the unit circle, i.e. angles that end at ?/6   .  Recall that all this says is that we begin at ?/6  then rotate around in the counter-clockwise direction (n is +ve) or clockwise direction (n is -ve) for n complete rotations. The similar thing can be done for the second solution.

Thus, all together the complete solution to this problem is following

                   ?/6  + 2 ? n  , n  =0, ± 1, ± 2, ± 3,.............

                  11?/6  + 2 ? n  , n  =0, ± 1, ± 2, ± 3,.............

As a last thought, notice that we can get - ?/6 by using n = -1 in the second solution.