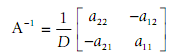Solving 2 × 2 systems of equations:

However this may be easy in a MATLAB, in normal finding solutions to the systems of equations is not. The systems which are 2 × 2 are, though, fairly clear-cut, and there are many methods of solution for such systems for which the MATLAB has built-in functions.

Consider the 2×2 system of equations which is as shown below:

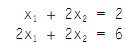
At first, to visualize the solution, it will be simpler to change both the equations to equation of a straight line by writing each in the form y = mx + b (by altering x₁ to x and x₂ to y):

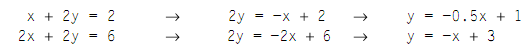
In MATLAB we can plot these lines by using a script; the answers are shown in figure.

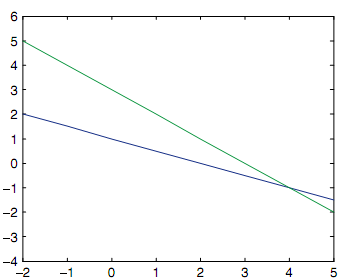
The intersection of the lines is the point (4, -1). In another words, x = 4 and y = -1. Altering back to x₁ and x₂, we hold x₁ = 4 and x₂ = -1. This permits us to visualize the solution.

This system of equations in a matrix form is as shown below:

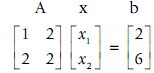
We know that the solution is x = A^-1 b, therefore we solve this when we can find the inverse of A. The one technique of finding the inverse for a 2 × 2 matrix includes computing the determinant D.

´ For a 2× 2matrix A=

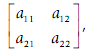
The determinant D is defined as follows:

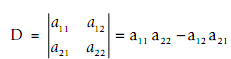
It is written by using vertical lines around the coefficients of the matrix, and is defined as the product of the values on the diagonal minus the product of the other two numbers.

For a 2 × 2 matrix, the matrix inverse is defined in terms of D as shown below: