Solve the subsequent quadratic equation:

Solve the subsequent quadratic equation through taking the square roots of both sides.

3x² = 100 - x²

Solution:

Step 1. Using the addition axiom, add x² to both sides of the equation.

3x²  + x²          = 100 - x²  + x²

4x²       = 100

Step 2. Using the division axiom, divide both sides of the equation through 4.

4x ² /4 = 100/4

x²  = 25

Step 3. Take the square root of both sides of the equation.

x²         = 25

√x²       = √25

x          = ±5

Thus, the roots are x = +5 and x = -5.

Step 4. Check the roots.

3x²       = 100 - x²

3(±5)²  = 100 - (±5)²

3(25)    = 100 - 25

75        = 75

If a pure quadratic equation is written in common form, a general expression can be written for its roots.  The common form of a pure quadratic is the subsequent.

ax² + c = 0                                                                 

Using the subtraction axiom and subtract c from both sides of the equation.

ax² = -c

Using the division axiom and divide both sides of the equation by a.

x²  = - c/a

Now take the square roots of both sides of the equation.

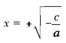
Therefore, the roots of a pure quadratic equation written in common form ax² + c = 0 are 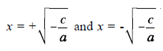.