Solve the subsequent IVP

Y'' - 9 y = 0, y(0) = 2, y'(0) = -1

Solution

First, the two functions

 y (t ) = e^3t  and  y(t ) = e^-3t

That is "nice enough" for us to by the general solution to the differential equation. At this point, please only believe this. You will be capable to verify this for yourself in a couple of sections.

The general solution to our differential equation is now,

y (t ) = c₁ e^-3t  + c₂e^3t

Here all we require to do is apply the initial conditions. It means that we require the derivative of the solution.

y' (t ) = -3 e^-3t  + 3e^3t

Plug in the initial conditions

2 = y (0) = c₁ + c₂

-1 = y'(0) = -3 c₁ +3 c₂

This provides us a system of two equations and two unknowns which can be solved.  Doing this yields

c₁ = 7/6, c₂ = 5/6

The solution to the IVP is so,

 y(t) = (7/6)e^-3t + (5/6) e^3t

Up to such point we've only looked at a particular differential equation and we found its solution by inspection. For rare little differential equations we can do this. Though, for the huge majority of the second order differential equations out there we will be not capable to do this.

Therefore, we would like a method for arriving at the two solutions we will require so as to form a general solution which will work for any linear, second order differential equation and constant coefficient equation. It is easier than it might initially look.

We will utilize the solutions we found in the first illustration as a guide. Each of the solutions in this illustration were in the form

y (t ) = e^rt

Remember, that we didn't include a constant in front of it as we can literally comprise any constant which we want and still get a solution. The significant idea here is to find the exponential function. One time we have which we can add on constants to our hearts content.

Thus, let's suppose that all solutions to,

ay′′ + by′ + cy = 0   ...................(4)

It will be of the form as

y (t ) = e rt        ........................(5)

To notice if we are correct all we require to do is plug this in the differential equation and notice what occurs.  Thus, let's get several derivatives and after that plug in.

y′ (t )= re^rt

 y′′ (t ) = r²e^rt

 a (r²e_rt )+ b (re^rt )+ c (e^rt ) = 0

e^rt (ar² + br + c )= 0

Therefore, if (5) is to be a solution to (4) then the subsequent must be true

e^rt (ar² + br + c ) = 0

It can be decreased further by noting as exponentials are never zero. Thus, (5) will be a solution to (4) given r is a solution to

 ar² + br + c = 0    .......... (6)

 This equation is usually termed as the characteristic equation for (4).

Okay, then how do we use this to get solutions to a linear, constant coefficient, second order differential equation? First write down the feature equation, (6), for the differential equation, (4). It will be a quadratic equation and thus we must expect two roots, r₁ and r₂. One time we have these two roots we have two solutions to the differential equation.

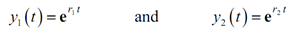...............(7)