Solve 9 sin ( 2 x )= -5 cos(2x ) on[-10,0].

Solution

At first glance this problem appears to be at odds with the sentence preceding the example. However, it really isn't.

Firstly, while we have more than one trig function in an equation we required a way to obtain equations that only include one trig function. There are several ways of doing this that depend on the type of equation we're beginning with. In this case we can just divide both sides by a cosine and we'll get a single tangent in the equation. Now we can see that this really is an equation that doesn't includes a sine or a cosine.

Hence, let's get begun on this example.

sin( 2x )/cos(x) =  tan ( 2x)  - =(5/9)   ⇒2x = tan ^-1( - 5/9)= -0.5071

Now, the unit circle doesn't involve tangents, however we can use it to illustrate the second angle in the range [0, 2π] .

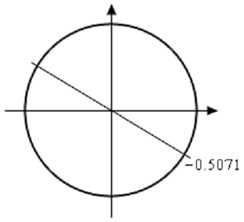
The angles that we're looking for here are those whose quotient of sine/cosine is the similar.  The second angle where we will get the similar value of tangent will be accurately opposite of the given point.  For this angle the values of sine & cosine are the similar except they will have opposite signs.  In the quotient however, the difference in signs will cancel out & we'll get the similar value of tangent.  Therefore, the second angle will always be the first angle plus π .

Before getting the second angle let's also note down that, such as the previous example, we'll use the 2π - 0.5071 = 5.7761 for the first angle.  Again, it is only due to a concern about losing track of the minus sign in our calculator answer. We could just as easily do the work with the original angle our calculator gave us.

Now, it is where is seems like we're just randomly making changes and doing things for no reason. The second angle that we're going to utilizes is,

                       π+( -0.5071)=π - 0.5071 = 2.6345

The fact that we utilized the calculator answer here seems to contradict the fact which we used a different angle for the first above.  The cause for doing this here is to give a second angle i.e. in the range [0, 2π] .  Had we utilized 5.7761 to determine the second angle we'd get π+ 5.7761 =8.9177.It is a perfectly acceptable answer, though it is larger than 2π (6.2832) and the general rule of thumb is to keep the initial angles as small as possible.

Following are all the solutions to the equation.

2x= 5.7761 +2π n        x = 2.8881 +π n ⇒

2x = 2.6345 + 2π n      x = 1.3173 +π nn= 0, ±1, ±2,.........

 n = -4  :x = -9.6783and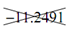

n = -3  :x = -6.5367   and-8.1075

n = -2 :x = -3.3951    and-4.9659

n = -1 :x = -0.2535    and-1.8243

n = 0    :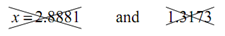 

Then the seven solutions to this equation are,

-0.2535, -1.8243, - 3.3951, - 4.9659, - 6.5367, - 8.1075,- 9.6783

Note that we didn't need to do the n=0 and computation as we could see from the given interval that we just wanted negative answers & these would clearly give positive answers.