Solve 6 sin ( x/2)= 1 on [-20,30]

Solution

Let's first work out calculator of the way since that isn't where the difference comes into play.

sin( x/2)= 1/6   ⇒x/2= sin ^-1( 1/6)= 0.1674

Here's a unit circle for this instance.

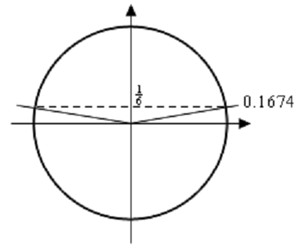
To determine the second angle in this case we can notice that the line in the first quadrant makes an angle of 0.1674 with the +ve x-axis and hence the angle in the second quadrant will then make an angle of 0.1674 with the -ve x-axis and hence the angle that we're after is then,

π - 0.1674 =2.9742 .

Here's the rest of the solution for this instance.  We're going to assume from this point on that you can do this work without much explanation.

x/2= 0.1674  + 2π n  ⇒         x = 0.3348 + 4π n          n= 0, ±1, ±2,.......

x/2= 2.9742 ± 2π nx = 5.9484 ± 4π n

n= -2 :x =  -24.7980 and   -19.1844

n = -1 :x = -12.2316  and  -6.6180

n = 0    : x = 0.3348    and      5.9484

n = 1    : x =12.9012    and      18.5148

n = 2    :x = 25.4676   and      31.0812

The solutions to this equation are then,

 x = -19.1844, -12.2316, - 6.6180, 0.3348, 5.9484, 12.9012, 18.5128, 25.4676

Note that in the previous instance we only got a single solution. It happens on occasion thus don't get worried regarding it. Also, note that it was the second angle which gave this solution and hence if we'd just relied on our calculator without worrying regarding other angles we would not have gotten this solution.  Again, it can't be stressed sufficient that whereas calculators are a great tool if we don't understand how to properly interpret/use the result we can (and frequently will) get the solution wrong.

To this point we've only worked examples including sine & cosine. Nowlet's work a couple of instance that involves other trig functions to see how they work.