Solve -10 cos(3t )= 7 on [-2,5].

Solution

Let's first get the inverse cosine portion of this problem taken care of.

cos(3 t )= -  7/10            ⇒     3t = cos^-1( - 7 )= 2.3462

Don't forget that still we need the "3"!

Now, let's look at a rapid unit circle for this problem.  Since we can illustrates the angle 2.3462 radians is in the second quadrant and the other angle that we need is in the third quadrant. We can find this second angle in accurately the same way we did in the previous instance. We can use either -2.346vor we can utilizes 2π - 2.3462 =3.9370.  As with the previous instance we'll utilizes the positive choice, however that is purely a matter of preference.  You could utilize the negative if you wanted to.

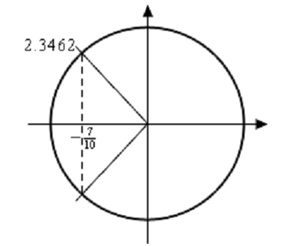
Thus, let's now finish out the problem.  Firstly, let's acknowledge that the values of 3t that we need are,

3t = 2.3462 + 2π n

3t = 3.9370+ 2π n

n = 0, ±1,±2,.........

Now, we have to properly deal along with the 3, hence divide that out to get all the solutions to the trig equation.

t = 0.7821 +(2π n/3)

t = 1.3123 +(2πn/3)

n = 0, ±1, ±2,..........

At last , we have to get the values in the given interval.

n = -2 : 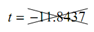           and           -2.8765

 n = -1 :t = -1.3123    and               -0.7821

n = 0    :t = 0.7821       and      1.3123

n = 1    :t = 2.8765       and      3.4067

n = 2    :                                t =4.9709            and      5.5011

The solutions to this equation, in the specified interval are then,

t = -1.3123, - 0.7821, 0.7821, 1.3123, 2.8765, 3.4067, 4.9709

We've done a couple of basic problems with cosines, now let's take a look at how solving equations with sines work.