The elasticity of a demand curve is frequently judged by its appearance: the flatter the demand curve, the greater the elasticity and vice versa. However this conclusion is misleading since two demand curves with different slopes may have the same elasticity at a given price. Actually, what appearance of a demand curve reveals is its slope, not the elasticity. Slope of the demand curve is marginal relationship between change in price (ΔP) and change in quantity demanded (ΔQ). Slope of demand curve is expressed as ΔP/ΔQ. It's the reciprocal of the slope ΔQ/ΔP that appears in the elasticity formula, not the slope itself.

We will illustrate below:

(i) that demand curves having different slopes can have the same elasticity at a given price and

(ii) Demand curves having the same slope can have different elasticity at a given price.Let's first explain that two demand curves with different slops can have the same elasticity at a given price. In Fig. below, demand curves AB and AD have different slopes. It can be proved as follows:

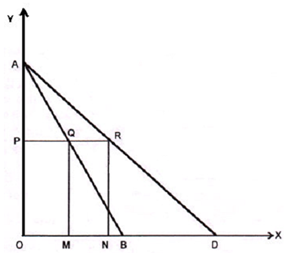
Figure: Demand Curves having different slopes

Slope of the demand curve AB=OA/OB and

Slope of the demand curve AD=OA/OD

Note that in these ratios, numerator OA is common to both the fractions, however in case of denominators OB

Consequently, OA/OB < OA/OD

Obviously, slopes of the two demand curves are different. Let's now show, that at a given price, both the demand curves have same elasticity. As illustrated in Fig. at a given price OP, the relevant points for measuring the elasticity are Q and R on the demand curves AB and AD, correspondingly. Recall that elasticity at a point on a linear demand curve is attained as  

e_p = Lower segment/ upper segment

So, at point Q on demand curve AB, e_p=QB/QA and at point R on AD, e_p=RD/RA

Therefore, at point Q on demand curve AB, e_p = QB/QA and at point R on AD, e_p = RD/RA.