Sketch (draw) the parametric curve for the subsequent set of parametric equations.
x = t2 + t
y = 2t -1
Solution
At this point our simply option for sketching a parametric curve is to pick up values of t, plug those values into the parametric equations and after that plot the points. Thus, let's plug in some t's.
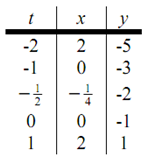
In the above first question that should be asked at this point is, how did we make out to use the values of t that we did, particularly the third choice? Although there is no real silution to this question, we just simply pick t's till we are fairly confident that we have got a good thought of what the curve looks like. It is this trouble along with picking "good" values of t that make out this method of sketching parametric curves one of the poorer selections. Occasionally we have no choice, though if we do have a choice we should avoid it.
We have an additional idea to discuss before we in fact sketch the curve. Parametric curves comprise a direction of motion. The direction of motion is specified by increasing t. Thus, when plotting parametric curves we as well involve arrows that show the direction of motion. We will frequently give the value of t that gave particular points on the graph also to make it clear the value of t that gave that specific point.
Now here is the diagram of this parametric curve.
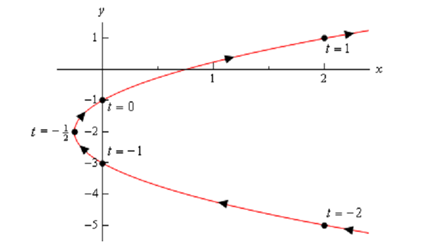
Thus, it looks like we have a parabola which opens to the right. Previous to we end this illustration there is a somewhat significant and subtle point that we require to discuss first. Notice that we ensure to involve a portion of the diagram to the right of the points corresponding to t = -2 and t = 1 to point out that there are portions of the diagram there.
Had we just stopped the sketch at those points we are pointing out that there was no portion of the curve to the right of those points and there evidently will be. We just didn't calculate any of those points.