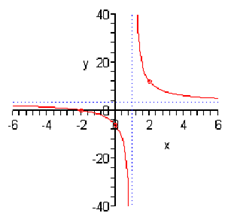
Sketch the graph of function.

f ( x ) =3x + 6 /x -1

Solution

Thus, we'll start off with the intercepts. The y-intercept is,

      f (0) =6/-1=-6⇒     (0, -6)

The x-intercepts will be,

3x + 6 = 0

x = -2                   ⇒ ( -2, 0)

Now, we have to determine the asymptotes.  Let's first determine the vertical asymptotes.

x -1 =0                 ⇒   x = 1

Thus, we've got one vertical asymptote. It means that now there are two regions of x's. They are x < 1 and x > 1 .

Now, the largest exponent within the numerator & denominator is 1 and thus by the fact there will be a horizontal asymptote at the line.

                                                   y = 3/1 = 3

Now, we only need points in each region of x's.  As the y-intercept & x-intercept are already in the left region we won't have to get any points there.  It means that we'll only need to get a point in the right region.  It doesn't actually matter what value of x we pick here we only have to keep it rather small so it will fit onto our graph.

f ( 2) = 3( 2) + 6/2 -1 = 12 /1= 12   ⇒  ( 2,12)

Putting all this together illustrate the following graph.