Single Point Perspective Transformation - Viewing Transformations

In order to derive the particular point perspective transformations beside the x and y-axes, we construct figures (19) and (20) as the same to the Figure 18, although with the consequent COP's at E(-d,0,0) and E(0,-d,0) on the -ive x and y-axes respectively.

The parametric equation of an l i.e. line EP, starting by E and passing through P is:

E+t(P-E)  0

=(-d,0,0)+t[(x,y,z)-(-d,0,0)]

=(-d,0,0)+t[x+d,y,z]

=[-d+t.(x+d), t.y, t.z]

Point P' is acquired, while t=t*

There is, P'=(x',y',z') =[-d+t*.(x+d), t*.y, t*.z]

Because, P' lies on X=0 plane shows -d+t*.(x+d)=0 must be true, which is t*=d/(x+d) is actual.

Hence, x'=-d+t*(x+d)=0

         y'=t*.y=y.d/(x+d)

         z'=t*.z=z.d/(x+d)

Hence P'=( 0, y.d/(z+d), z.d/(x+d))

          = (0,y/((z/d)+1), z/((x/d)+1))

In terms of Homogeneous coordinate system as P'=(0,y,z,(x/d)+1). The above equation can become in matrix form that is: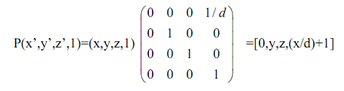

=[0,y/((z/d)+1), z/((x/d)+1),1] -------- (5)

is, P'_h = P_h.P_per,x  --------------------------------(6)

Here P_per,z    in equation (5) implies the particular point perspective transformation w.r.t. x-axis.

Thus, the ordinary coordinates projected point P' of a agreed point P of a particular point perspective transformation with respect to the x-axis as:

(x', y',z',1)= [0,y/((z/d)+1), z/((x/d)+1),1] which has a center of projection at [-d,0,0,1] and a vanishing point assigned on the x-axis at [0,0,0,1]

As the same, the particular point perspective transformation w.r.t. y-axis is consequently:

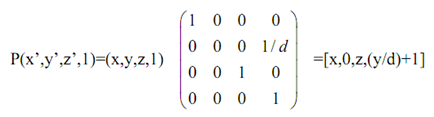
=[x/((y/d)+1),0, z/((y/d)+1),1] That is, P'h = Ph.Pper,y  -----------------------------(7)

Here P_per,y  in equation (5) implies the particular point perspective transformation w.r.t. y-axis.

Hence, the ordinary coordinates as projected point P' of a given point P of a particular point perspective transformation w.r.t. y-axis that is:

(x',y',z',1)=[x/((y/d)+1),0, z/((y/d)+1),1] which has a center of projection at [0,-d,0,1] and a vanishing point assigned on the y-axis at [0,0,0,1].