Method to solve Simultaneous Equations with two or more than two variables

Method 

Above we have seen equations wherein we are required to find the value of the variable x only. Apart from the equations of the type we have seen above, simple equations of the form 7x + 2y = 47 also exists. As against the equations x - 3 = 12 or 3x + 5 = 20 where we had a single variable x, we have two variables x and y. If we express this equation in terms of y it will be

                   7x + 2y                = 47

                   7x - 7x + 2y          = 47 - 7x

                   0 + 2y                  = 47 - 7x

                    2y                      = 47 - 7x

In this expression by giving values to x and solving the expression we get corresponding values for y.

Now if another equation of the form 5x - 4y = 1 is expressed in terms of y, we have

y

=

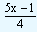For this equation also if we substitute values for x, we would get corresponding values for y.

At this stage if we want values which satisfy both the equations then the values of y in both these equations should be identical. That is,

On cross multiplying, we have 4(47 - 7x) = 2(5x - 1)

                   188 - 28x = 10x - 2

Collecting all x terms and constants, we have

                 -10x - 28x    =    - 2 - 188

                         -38x    =    - 190

                              x    =       5

We substitute this value of x = 5, in either of equations to get the value of y.

                   5x - 4y     =     1

                   5(5) - 4y  =     1

                   - 4y         =     1 - 25

                   - 4y         =       - 24

                       y         =       -24/ - 4 = 6.

Therefore, the common values of x and y which satisfy these two equations simultaneously are x = 5 and y = 6. Therefore, we can define simultaneous equations as two or more equations which are satisfied by the same values of x and y (unknown quantities).