Simpson's Rule - Approximating Definite Integrals

This is the last method we're going to take a look at and in this case we will once again divide up the interval [a, b] into n subintervals.  Though, unlike the preceding two methods we want to require that n be even. The cause for this will be obvious in a bit. The width of every subinterval is,

Δx = b - a / n

In the Trapezoid Rule (explain earlier) we approximated the curve along with a straight line.  For this Rule (Simpson's Rule) we are going to approximate the function along with a quadratic and we're going to need that the quadratic agree with three of the points from our subintervals.  Below is a drawing of this using n = 6.  Every approximation is colored in a different way thus we can see how they actually work.

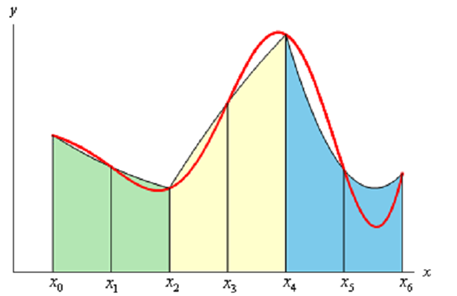
Note: In fact each approximation covers two of the subintervals. This is the cause for requiring n to be even.  A few approximations look much more like a line after that a quadratic, but they really are quadratics. As well note that some of the approximations do a better job as compared to others. It can be illustrated that the area under the approximation on the intervals [x_{i -1}, x_i] and [x_i , x_i+1] Δ is like this:

A_i = Δx / 3 (f(x_i-1)+4f(x_i) + f (x_i+1))

If we make use of n subintervals the integral is then approximately,

 ∫^b_a  f (x) dx ≈  Δx / 3 (f(x₀) + 4f (x₁) + f (x₂) + Δx / 3  (f (x₂) + 4f (x₃) + f (x₄)) + ....+ Δx / 3 (f (x_n-₂) + 4f (x_n-1) + f (x_n))  

On simplifying we reach at the general Simpson's Rule.

 ∫_a^b   f (x) dx ≈ Δx / 3 [(f(x₀) + 4f (x₁) + 2f (x₂) .... + 2f (x_n-2) + 4f (x_n-1) + f(x_n)]

In the above case notice that all the function evaluations at points along with odd subscripts are multiplied by 4 and every function evaluations at points with even subscripts (apart from for the first and last) are multiplied by 2.  If you can keep in mind this, this is a quite easy rule to remember.