Simply supported beam - Shear Force diagram:

A simply supported beam of length 8 m is subjected to a consistently varying load from zero at centre to 3 t/m at both of ends. Draw the BMD and SFD.

Solution

Taking moment around A,

R _B  × 8 - (½) × 4 × 3 (4 × (2/3) × 4 ) - 1 × 4 × 3( (1/3) × 4 )  = 0

R_B = 6 t

R   = ( (½) × 4 × 3) × 2 - R _B     = 12 - 6 = 60

On the other hand, since the load is symmetrical, the reaction at the support shall be equal to half of the entire downward load.

R_A  = R_B  = 6 t

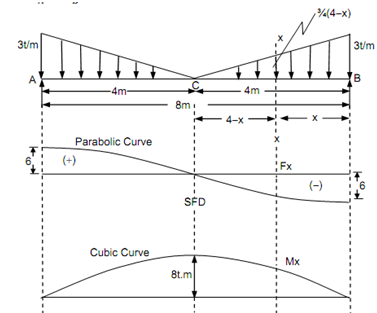
Figure

Shear Force

SF at A,          F_A  = +6t          

SF at C,                    F_A   =+ 6 - (½) × 4 × 3 = 0

SF at B,                      F_B   = 0 - (1 /2)× 4 × 3 = - 6 t  = Reaction at B.

 To determine the form of SFD, let a section XX at a distance 'x' from the end B.

F _x  =- 6 + (½) × x × ( 3 + (3 /4)(4 - x) )

   =- 6 + (½) × x × (12 + 3 (4 - x) /4)

F _x =- 6 +(x/8) × (12 + 12 - 3x) =- (48 + 24 x - 3x² )/8

As, the SF equation is parabolic equation, the SFD is in the form of parabolic curve.

Bending Moment

BM at A and B, MA = MB = 0

BM at C, M _C = (6 × 4) - ( (½) × 4 × 3 × (2/3) × 4 )= 24 - 16 = 8 t m

Maximum bending moment take place at centre, as, the SF is zero at centre of the beam.

Bending moment at XX,

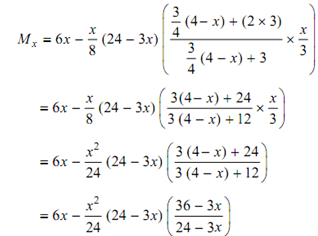
          = 6x-( x²/24)(36-3x)

          = 6x- (3x²/24)-(3x³/24)

         M_x = 6x - (3x²/2)-(x³/8)

This equation denoted that the bending moment diagram is in the form of cubic curve.